2. Basics of Simple Linear Regression#
本课程前置需要装的包:
require(s20x)
Show code cell output
载入需要的程辑包:s20x
2.1. 分析数据过程#
2.1.1. 读取数据#
读取数据表格,header=TRUE 表示第一行是表头,sep="," 表示分隔符是逗号。
course.df <- read.table("../data/STATS20x.txt", header = TRUE, sep = "\t")
head(course.df) # 看前面大约10行的内容
dim(course.df) # 看有多少行、多少列
course.df$Exam[1:20] # 看前20行的Exam列
| Grade | Pass | Exam | Degree | Gender | Attend | Assign | Test | B | C | MC | Colour | Stage1 | Years.Since | Repeat | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| <chr> | <chr> | <int> | <chr> | <chr> | <chr> | <dbl> | <dbl> | <int> | <int> | <int> | <chr> | <chr> | <dbl> | <chr> | |
| 1 | C | Yes | 42 | BSc | Male | Yes | 17.2 | 9.1 | 5 | 13 | 12 | Blue | C | 2.5 | Yes |
| 2 | B | Yes | 58 | BCom | Female | Yes | 17.2 | 13.6 | 12 | 12 | 17 | Yellow | A | 2.0 | No |
| 3 | A | Yes | 81 | Other | Female | Yes | 17.2 | 14.5 | 14 | 17 | 25 | Blue | A | 3.0 | No |
| 4 | A | Yes | 86 | Other | Female | Yes | 19.6 | 19.1 | 15 | 17 | 27 | Yellow | A | 0.0 | No |
| 5 | D | No | 35 | Other | Male | No | 8.0 | 8.2 | 4 | 1 | 15 | Blue | C | 3.0 | No |
| 6 | A | Yes | 72 | BCom | Female | Yes | 18.4 | 12.7 | 15 | 17 | 20 | Blue | A | 1.5 | No |
- 146
- 15
- 42
- 58
- 81
- 86
- 35
- 72
- 42
- 25
- 36
- 48
- 29
- 54
- 49
- 52
- 28
- 34
- 51
- 81
- 80
- 41
2.1.2. 绘图观测数据#
对数据进行绘图分析,着重分析 Exam 和 Test 两个变量之间的关系。
首先应当粗略查看两者的关系,如线性、二次、曲线、正弦等
library(s20x)
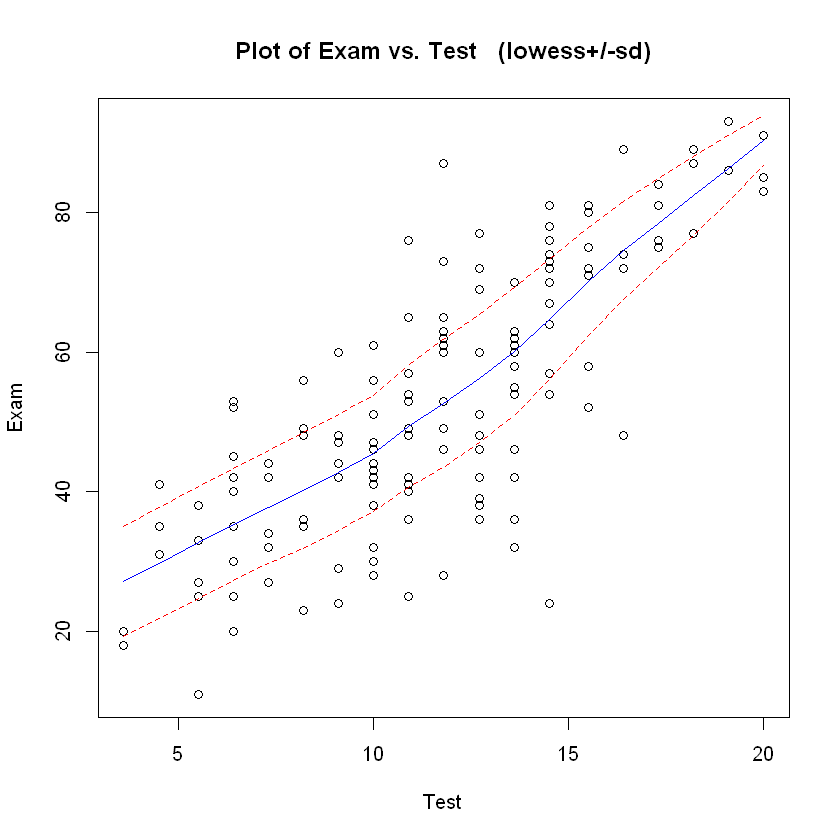
trendscatter(Exam ~ Test, data = course.df)
2.1.3. 进行初步拟合#
可以看到整体大致呈线性关系,故我们采用线性回归模型。
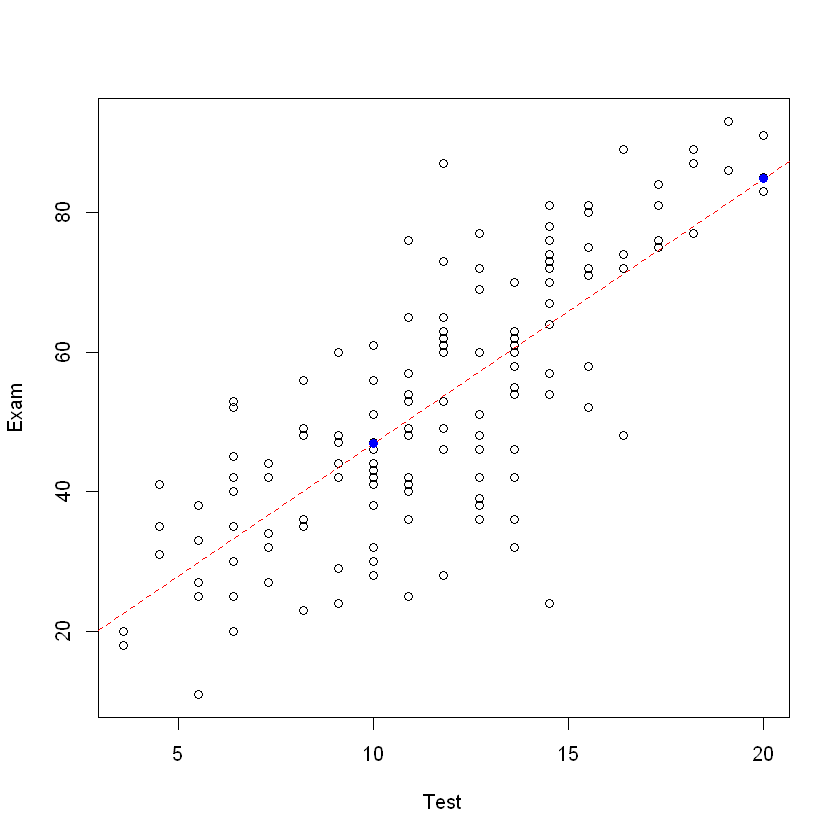
plot(Exam ~ Test, data = course.df)
# 绘制回归直线
examtest.fit <- lm(Exam ~ Test, data = course.df)
# lty = 2 表示虚线,col = "red" 表示红色
abline(examtest.fit, lty = 2, col = "red")
points(
0,
predict(examtest.fit, newdata = data.frame(Test = 0)),
col = "blue",
pch = 19
)
points(10, predict(examtest.fit,
newdata = data.frame(Test = 10)
), col = "blue", pch = 19)
points(20, predict(examtest.fit,
newdata = data.frame(Test = 20)
), col = "blue", pch = 19)
summary(examtest.fit)
Call:
lm(formula = Exam ~ Test, data = course.df)
Residuals:
Min 1Q Median 3Q Max
-39.980 -6.471 0.826 8.575 33.242
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 9.0845 3.2204 2.821 0.00547 **
Test 3.7859 0.2647 14.301 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 12.05 on 144 degrees of freedom
Multiple R-squared: 0.5868, Adjusted R-squared: 0.5839
F-statistic: 204.5 on 1 and 144 DF, p-value: < 2.2e-16
其中:
Call:表示回归方程,指明了自变量和因变量
Risiduals:残差,指明了残差的分布,如最大、最小、中值等
Coefficients:系数,此处即 \(a_i\) 和 \(b_i\) 的值
Residual standard error:残差标准差,即残差的标准差
Multiple R-squared:多元 \(R^2\) 值
Adjusted R-squared:调整后的 \(R^2\) 值
F-statistic:F 统计量,即 F 统计量。F 统计量的分子是回归平方和,分母是残差平方和。F 统计量的值越大,说明回归平方和越大,即回归模型的拟合效果越好。F 统计量的值越小,说明回归平方和越小,即回归模型的拟合效果越差。p-value 则相反。
2.2. 分析数据是否可以接受#
2.2.1. 残差观测#
针对指定行分析预测值和残差:
data.frame(course.df$Test[1], course.df$Exam[1]) # 原第一行
# 按照 tidyverse 的风格,也可以使用 dplyr 包的 select 函数来选择列
# dplyr::select(course.df[1, ], Exam, Test)
fitted(examtest.fit)[1] # 拟合值
resid(examtest.fit)[1] # 残差
| course.df.Test.1. | course.df.Exam.1. |
|---|---|
| <dbl> | <int> |
| 9.1 | 42 |
检验上,一个成功的拟合模型的残差应当有:
残差均值接近于 0
残差满足正态分布
没有或排除了异常点
2.2.1.1. 残差均值接近于 0#
分析残差,看是否符合均值等于0
# 其中 which = 1 表示残差直方图(histogram of residuals),
# which = 2 表示残差QQ图(qqplot,即 normal quantile-quantile-plot),
# which = 3 表示残差标准化图
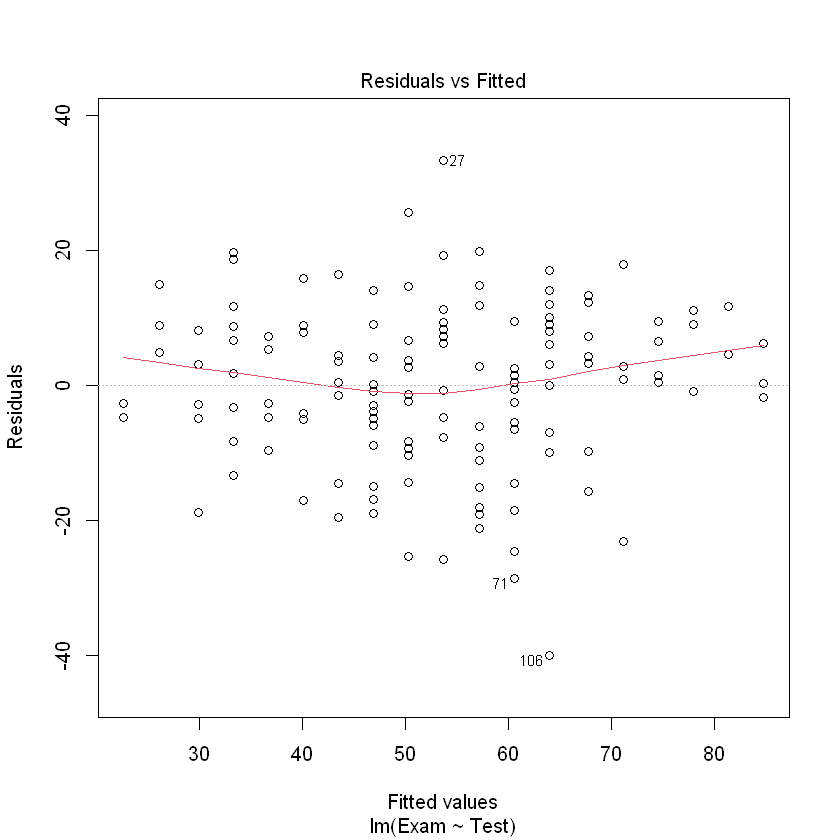
plot(examtest.fit, which = 1)
2.2.1.2. 残差满足正态分布#
残差在分布上在符合正态同分布:iid – independence(并且这是根据学生在考试中应该相互独立的表现)。残差应该有大致恒定的散布。这其实是 Equality Of Variance (EOV,方差相等) 原则。
检查残差是否满足正态分布:
normcheck(examtest.fit)
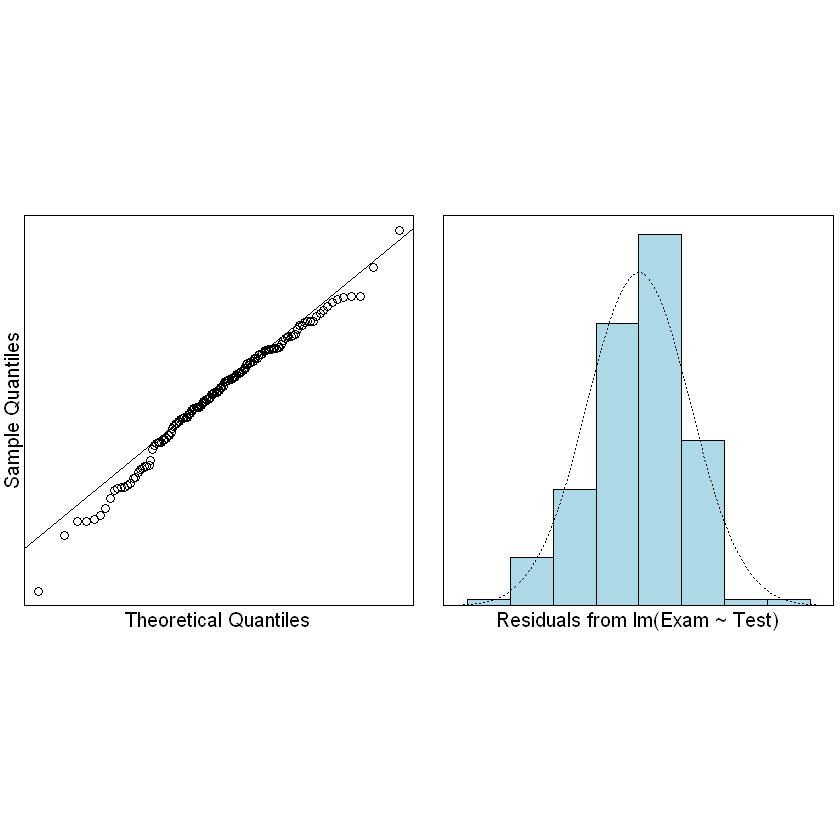
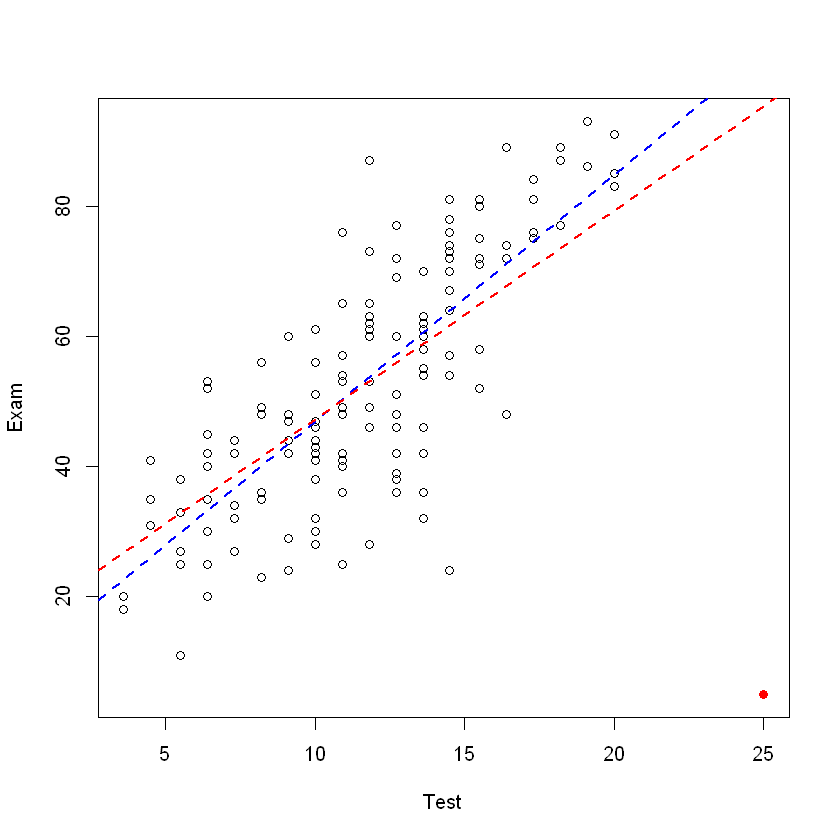
# 创造一个包含异常点的数据集并验证异常点对回归直线的影响
n <- nrow(course.df)
# 复制一数据集的最后一行
course2.df <- course.df[c(1:n, n), ]
# 修改新数据集的最后一行的 Test 和 Exam 列的值,故意创造一个差异极大的观测值
course2.df[n + 1, c("Test", "Exam")] <- c(25, 5)
# 画出散点图
plot(Exam ~ Test, data = course2.df)
## 并标记我们创建的新的观测点
points(25, 5, pch = 19, col = "red")
# 如果有的观测值是异常值,那么回归直线就会受到影响
examtest2.fit <- lm(Exam ~ Test, data = course2.df)
summary(examtest2.fit)
# 或者直接画图验证该点造成的影响
abline(examtest.fit, lty = 2, lwd = 2, col = "blue")
abline(examtest2.fit, lty = 2, lwd = 2, col = "red")
Call:
lm(formula = Exam ~ Test, data = course2.df)
Residuals:
Min 1Q Median 3Q Max
-90.251 -6.846 2.638 9.456 33.996
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 15.2374 3.7172 4.099 6.88e-05 ***
Test 3.2006 0.3023 10.588 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 14.34 on 145 degrees of freedom
Multiple R-squared: 0.436, Adjusted R-squared: 0.4322
F-statistic: 112.1 on 1 and 145 DF, p-value: < 2.2e-16
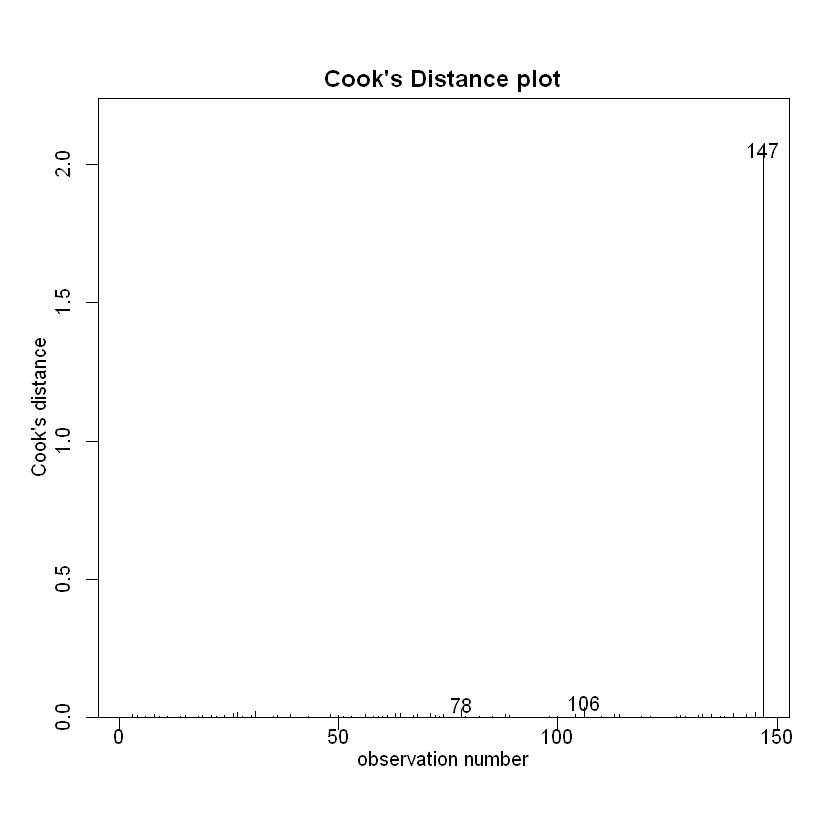
对其进行观测值差异分析:
# 画出异常值的影响
cooks20x(examtest2.fit)
# 对比原来的值影响
cooks20x(examtest.fit)
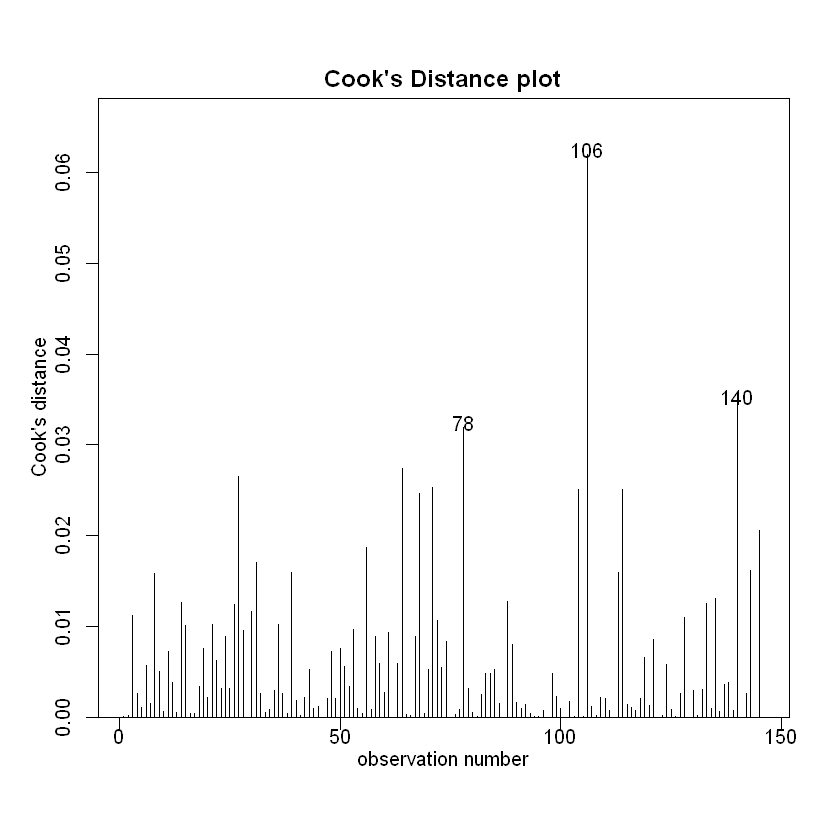
2.2.2. R 方观测#
R Squared 即 R 平方,是回归平方和与总平方和的比值,即 \(R^2 = \frac{SSR}{SST}\),其中 SSR 为回归平方和,SST 为总平方和。R 平方的值越大,说明回归平方和越大,即回归模型的拟合效果越好。R 平方的值越小,说明回归平方和越小,即回归模型的拟合效果越差。
SSR 即回归平方和,是因变量的预测值与因变量的均值之差的平方和,即 \(SSR = \sum_{i=1}^n (y_i - \bar{y})^2\),其中 \(y_i\) 为第 \(i\) 个观测值,\(\bar{y}\) 为因变量的均值。下面将简要介绍 SSR 的计算方法。
# 消除一次项
examnull.fit <- lm(Exam ~ 1, data = course.df)
summary(examnull.fit)
# 对比之前的 Summary
summary(examtest.fit)
Call:
lm(formula = Exam ~ 1, data = course.df)
Residuals:
Min 1Q Median 3Q Max
-41.877 -12.877 -1.377 15.623 40.123
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 52.877 1.546 34.21 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 18.68 on 145 degrees of freedom
Call:
lm(formula = Exam ~ Test, data = course.df)
Residuals:
Min 1Q Median 3Q Max
-39.980 -6.471 0.826 8.575 33.242
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 9.0845 3.2204 2.821 0.00547 **
Test 3.7859 0.2647 14.301 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 12.05 on 144 degrees of freedom
Multiple R-squared: 0.5868, Adjusted R-squared: 0.5839
F-statistic: 204.5 on 1 and 144 DF, p-value: < 2.2e-16
此时我们可以得到 SS(Null)的值 18.68,以及 SS(Test)的值 12.05。
R 方的值即 1 - SS(Null)/SS(Test)的值,即 0.5868。
置信区间:\([a_i - 2SE(a_i), a_i + 2SE(a_i)]\),即 \([a_i - 2\sqrt{Var(a_i)}, a_i + 2\sqrt{Var(a_i)}]\),其中 \(Var(a_i)\) 为 \(a_i\) 的方差。
2.2.3. 每一个拟合值的 T 检验#
知道看什么,什么意思,怎么看
summary(examtest.fit)
Call:
lm(formula = Exam ~ Test, data = course.df)
Residuals:
Min 1Q Median 3Q Max
-39.980 -6.471 0.826 8.575 33.242
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 9.0845 3.2204 2.821 0.00547 **
Test 3.7859 0.2647 14.301 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 12.05 on 144 degrees of freedom
Multiple R-squared: 0.5868, Adjusted R-squared: 0.5839
F-statistic: 204.5 on 1 and 144 DF, p-value: < 2.2e-16
可以看出 Test 行的 Pr(P-value)的值小于 2.2x10^-16,远小于 0.05,故拒绝原假设,即拟合值的系(旁边的3颗*也表示可信度极高,即该斜率的线性拟合极好)
零假设 \(H_0\):Test 和 Exam 之间的线性关系系数为 0(没有线性关系),即 即 \(a_i\) 的系数为 0
备择假设 \(H_1\):Test 和 Exam 之间的线性关系系数不为 0(有线性关系),即 即 \(a_i\) 的系数不为 0
我们对于斜率的置信程度,是由标准误差决定的,即 \(SE(a_i)\),即 \(SE(a_i) = \sqrt{\frac{SSE}{n-2}}\),其中 SSE 为残差平方和,即 \(SSE = \sum_{i=1}^n (y_i - \hat{y_i})^2\),其中 \(\hat{y_i}\) 为第 \(i\) 个观测值的预测值,即 \(\hat{y_i} = a_i + b_i x_i\),\(x_i\) 为第 \(i\) 个观测值的自变量值。此处的 \(se(a)\) 为 0.2647。于是我们有:
此结果表示偏离此结果的标准差,这个数字越大,代表我们对于斜率的置信程度越高。
2.3. 利用分析结果做预测#
2.3.1. 拟合值的置信区间#
confint(examtest.fit)
# Intercept 即截距,Test 即斜率
# 也可以自己修改置信水平
confint(examtest.fit, level = 0.99)
| 2.5 % | 97.5 % | |
|---|---|---|
| (Intercept) | 2.719020 | 15.449907 |
| Test | 3.262659 | 4.309189 |
| 0.5 % | 99.5 % | |
|---|---|---|
| (Intercept) | 0.6778171 | 17.491110 |
| Test | 3.0948635 | 4.476984 |
2.3.2. 预测#
准确预测值
预测的均值范围
预测每一个个体的取值范围
区间估计和点估计的区别:
区间估计:给出一个区间,表示参数的可能取值范围
点估计:给出一个点,表示参数的可能取值
# 区间估计
preds.df <- data.frame(Test = seq(0, 20, by = 10))
predict(examtest.fit, newdata = preds.df, interval = "confidence")
# 点估计
predict(examtest.fit, newdata = preds.df, interval = "prediction")
| fit | lwr | upr | |
|---|---|---|---|
| 1 | 9.084463 | 2.71902 | 15.44991 |
| 2 | 46.943703 | 44.80912 | 49.07828 |
| 3 | 84.802942 | 79.97021 | 89.63568 |
| fit | lwr | upr | |
|---|---|---|---|
| 1 | 9.084463 | -15.56475 | 33.73368 |
| 2 | 46.943703 | 23.03510 | 70.85231 |
| 3 | 84.802942 | 60.50438 | 109.10151 |
其中:
区间估计表格的 [2,2:3] 表示所有半期考试10分,期末考试的分数的均值的范围
区间估计表格的 [2,2:3] 表示所有半期考试10分个体的分数的范围,落在这个范围即为正常值
2.4. 总结#
遇到此类问题,通用思路(适用于分析x和y两个未知数的某种关系):
绘制数据散点图并简要查看自变量与因变量之间是哪种关系(如果有关系),最好是能够通过工具分析(也可能会有一份研究意图的声明可以被指导)。提出适当的研究方式。在上边的例子中,我们就决定采用了线性模型:
\[ y = β_0 + β_1x_i + ε_i, ε_i ∼ N(0, σ^2) (where β_1 > 0) \]使用
lm函数进行模型拟合。检查我们提出的假设进行合适方式的验证。
Independence OK? (how were the data collected?)
EOV Okay? Using
plot(examtest.fit, which = 1).Normality Okay? Using
normcheck.
If these are okay then go to next step.
尝试适时删除任何不重要的解释变量(后面会讲)。如果能删除,请检查新的研究方式。
确保个别要点不会产生过分的不适当的影响,并尝试删除/纠正它们。Using
cooks20x.做出结论/预测,讨论极限,并回答相关的研究问题。
注意:在上述步骤中,在对当前步骤满意之前,切记不要匆忙进行下一步。
